다익스트라 알고리즘 (Dijkstra Algorithm)
1. 개념
다익스트라 (Dijkstra) 최단경로 알고리즘은 그래프에서 여러 개의 node가 있을 때,
특정 노드에서 출발하여 다른 모든 노드로 가는 최단 경로를 구해주는 알고리즘이다.
주의할 점은 다익스트라 알고리즘은 0보다 작은 '음의 간선' 이 있으면 정상적으로 동작하지 않는다는 점이다.
하지만 실제 현실세계의 길에는 '음의 간선' 이라는 것이 존재하지 않으므로, GPS 소프트웨어의 알고리즘으로 주로 사용되곤 한다.
2. 동작 과정
1) 출발 노드 설정
2) 최단거리 테이블 초기화
3) 방문하지 않는 노드들 중 최단거리가 가장 짧은 노드 선택
4) 해당 노드를 거쳐 다른 노드를 가는 비용을 계산하여 최단 거리 테이블 갱신
5) 3번 4번 반복
여기서 최단 거리 테이블이란 출발 노드에서 다른 노드에 대한 '현재까지의' 최단거리 정보를 가진 1차원 리스트 를 의미한다. 최단 경로를 구하는 과정에서 계속 당장 '현재' 의 최단거리가 짧은 노드를 확인하므로 그리디 알고리즘 에 속한다.
3. 동작 예
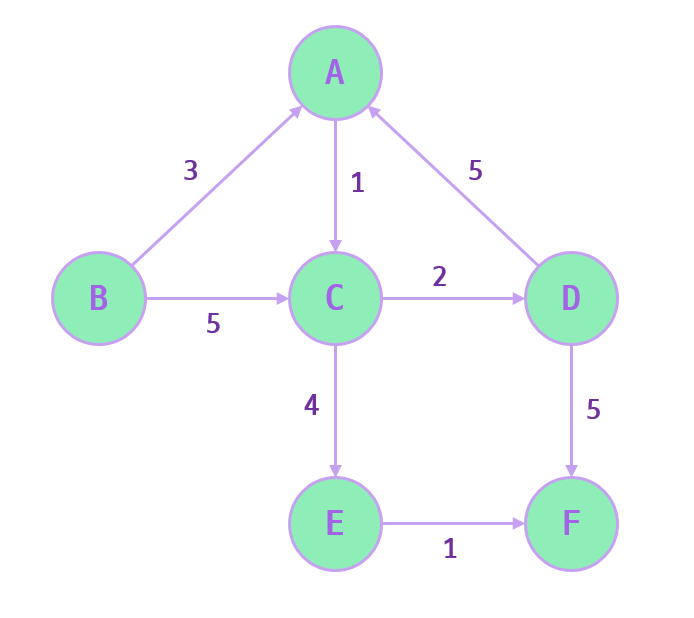
위 그래프에서 출발노드를 B 라고 하자.
최단경로 테이블을 초기화한다.
Active Vertex [ B ]
|
노드 |
A |
★B |
C |
D |
E |
F |
|
거리 |
INF |
0 |
INF |
INF |
INF |
INF |
현재 B와 연결된 A와 C중 최단거리가 가장 짧은 노드인 A를 선택하다.
Active Vertex [ B, A ]
|
노드 |
★A |
B |
C |
D |
E |
F |
|
거리 |
3 |
0 |
5 |
INF |
INF |
INF |
Active Vertix에 A가 추가되고 C의 최단거리가 4로 감소한다. Active Vertex 연결된 다른 노드가 없으므로 C를 선택한다.
Active Vertex [ B, A, C ]
|
노드 |
A |
B |
★C |
D |
E |
F |
|
거리 |
3 |
0 |
4 |
INF |
INF |
INF |
B -> A -> C -> D 로 D의 최단경로는 6
B -> A -> C -> E 로 E의 최단경로는 8
더 짧은 D를 선택한다.
Active Vertex [ B, A, C, D ]
|
노드 |
A |
B |
C |
★D |
E |
F |
|
거리 |
3 |
0 |
4 |
6 |
8 |
INF |
B -> A -> C -> D -> F 로 F의 최단경로는 11
E는 그대로 8이다.
더 짦은 E를 선택한다.
Active Vertex [ B, A, C, D, E ]
|
노드 |
A |
B |
C |
D |
★E |
F |
|
거리 |
3 |
0 |
4 |
6 |
8 |
11 |
E가 추가되면서 F의 최단경로가 단축된다.
B -> A -> C -> E -> F 로 F의 최단경로는 9
마지막 남은 F를 선택한다.
Active Vertex [ B, A, C, D, E, F ]
|
노드 |
A |
B |
C |
D |
E |
★F |
|
거리 |
3 |
0 |
4 |
6 |
8 |
9 |
최단경로 최종 간선 선택 결과는 다음과 같다.

관련글
다음은 다익스트라 알고리즘을 어떻게 구현할 것인지에 대한 것을 다뤄보고자 한다.
아래 게시글에 정리해두었다.
[ 알고리즘 개념 ] 다익스트라 알고리즘 (Dijkstra Algorithm) 구현 - 파이썬(Python)
다익스트라 알고리즘 (Dijkstra Algorithm) 구현 - 파이썬(Python) 다익스트라 알고리즘에 대한 개념은 이전 게시글에 정리해두었다. codingexplore.tistory.com/51?category=886802 [ 알고리즘 개념 ] 다익..
codingexplore.tistory.com
참고자료
slidetodoc.com/shortest-path-algorithm-what-is-the-shortest-path-2/
Shortest Path Algorithm What is the Shortest Path
What is the shortest path problem? • In an edge-weighted graph, the weight of an edge measures the cost of traveling that edge. • For example, in a graph representing a network of airports, the weights could represent: distance, cost or time. • Such
slidetodoc.com
'Algorithm > Algorithm Concepts' 카테고리의 다른 글
| [ 알고리즘 개념 ] 플로이드 워셜 알고리즘 (Floyd-Warshall Algorithm) (0) | 2021.05.12 |
|---|---|
| [ 알고리즘 개념 ] 다익스트라 알고리즘 (Dijkstra Algorithm) 구현 - 파이썬(Python) (0) | 2021.05.09 |
| [ 알고리즘 개념 ] 그래프 탐색 DFS/BFS 구현 - 파이썬(Python) (0) | 2021.05.02 |
| [ 알고리즘 개념 ] 분할정복 (Divide and Conquer) (0) | 2021.04.12 |
| [ 알고리즘 개념 ] 큐 (Queue), 덱(Deque) (0) | 2021.04.08 |
